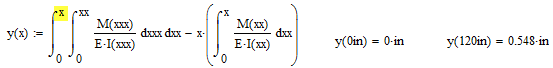Community Tip - Want the oppurtunity to discuss enhancements to PTC products? Join a working group! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Beam Deflection in a Tapered Pipe
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Beam Deflection in a Tapered Pipe
I need help comparing the deflection of pipe with two different cases. Case 1 is a regular non-tapering pipe. The case 2 is a tapered pipe that should deflect less than the straight pipe. I am working in MathCad and can change the value of my variables, so I have set the two cases to be equal to one another (by saying that the variable D.w is equal to D) for the sake of comparison. The answers should be equal to one another so I know that there is a problem but I am not sure where. I think that it is within setting up the double integral since I checked the case 1 pipe deflection against a different pipe deflection calculator. Any help would certainly be appreciated.
- Labels:
-
Calculus_Derivatives
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Which values should be the same? y1 and y2=y3?
The way you had setup your double integral is not desireable as in the inner integral you use x as intgration variable and as upper limit. The upper limit should be changed to another name and this would be the integration variable of the outer intgeral. Doing so does not change the result, though.
y1 and y3 would only be the same if x^2*(3*L-x)=L^3.
If you look at your definition of y3 you get (by symbolical evaluation)
L^3*W/(6*E*I)
and compare this to your definition of y1
W*x^2*(3*L-x)/(6*E*I)
So for L=x you are missing a factor 2 to get the same result with y3 as with y1.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
When you set Dw equal to D the integrals in y2 are easy to solve analytically (by hand). You get a result which is a factor of 2 different from y1, which is what the numerical results are telling you. Where you have pi/64 you should probably have pi/128
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In an effort to simplify the calc and let mathcad do the work, I defined (x=0) @ the free end and (L=x) at the fixed end and set up functions in terms of x. I also included graphs for the diameter, moment, moment of inertia, deflection angle, and deflection all in terms of x.
I think that the functions for diameter, moment and moment of inertia are correct. The deflection graph seems opposite what I expect in that @ x=0 the angle should be 0deg. Could that be due to the definite integration range? Should this change to something else?
The deflection graph crosses 0 so I know that can't be right.
I still think that I have an error in how I define the integrals.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Could it be that it should be that way?