Community Tip - Did you get an answer that solved your problem? Please mark it as an Accepted Solution so others with the same problem can find the answer easily. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Polar Coordinates
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Polar Coordinates
Does anyone know how to display complex calculated results in polar coordinates? I realize one can enter polar coordinates in complex calculations using Euler's formula, but MathCAD always returns the result in Cartesian coordinates. This is particularly annoying, especially if one is trying to compare the calculated values to the input values. If there isn't a way to do this, then I think it should be added as a feature to MathCAD. It's hard to imagine a software package as powerful (and expensive) as MathCAD not offering polar coordinates. We pay a fee annually to stay current with MathCAD, and I submitted this as a suggestion more than a year ago, but still haven't seen it. The entire power industry is a sector of the engineering industry that would benefit from this because we deal with polar coordinates all the time.
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It is built-in format in Mathcad Prime.
In Mathcad ** we can use user tool:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you, Valery. That is a very nice function - I tried it out and it parses X-Y coordinates nicely, returning polar values as a string. But I couldn't get it to force a calculated result to display in polar. MathCAD doesn't allow a final result to be manipulated with a function. I think I will have to wait until the powers that be decide to include a coordinate system display option feature. Even my 7-year-old graphing calculator allows the user to choose between rectangular, polar or spherical representation. Best regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is what I would suggest to MathCAD, if someone from MathCAD is paying attention. Include the coordinate system as a Worksheet Display Option choice (see below and note the pasted-in Coordinate System as an example):
A better alternative might be to include the coordinate system as a right-click option; the user could right-click on a complex equation and select the display coordinate system for that equation (again, note the pasted-in Coordinate System as an example):
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
What's wrong with the built in functions Mathcad has????
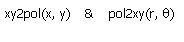
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You might like this I forgot to post it.

Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This is a very impressive function - I'm going to have to hang onto this. Thank you for posting it. Nevertheless, I respectfully maintain that MathCAD needs a Worksheet Option for "Coordinate System"; either that or (even better) an equation option for the same.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This is a very impressive function - I'm going to have to hang onto this. Thank you for posting it. Nevertheless, I respectfully maintain that MathCAD needs a Worksheet Option for "Coordinate System"; either that or (even better) an equation option for the same.
You know what to do then.
Post your request here. ![]()
http://communities.ptc.com/message/158000#158000
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The entire power industry is a sector of the engineering industry that would benefit from this because we deal with polar coordinates all the time.
That is a big statement saying the entire industry would benefit.
because we deal with polar coordinates all the time.
Sorry to be argumentative, but I actually use Cartesian, but I do agree that Mathcad should include a conversion.
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
While it is true that line impedance values are sometimes represented in rectangular coordinates (resistance, reactance), the vast majority of computations and analyses performed by power system engineers revolve around magnitude and phase angle, including: synchronism check, polarizing quantities, alpha plane calculations, symmetrical components, load encroachment, etc. One could say that power system analysis is very angle dependent, and the use of rectangular coordinates often inserts a degree of separation (no pun intended) between the output and what the engineer is ultimately looking for, requiring an extra step on the part of the engineer.
I'm familiar with the xy2pol() and pol2xy() functions that were mentioned, but as I pointed out above, one cannot apply a MathCAD function to a calculated result. If I want to find a zero-sequence quantity by adding vectorally the three complex phase quantities, MathCAD yields the result in Cartesian, and there isn't a function in existance that will deliver the answer in polar.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
but as I pointed out above, one cannot apply a MathCAD function to a calculated result.
Yes you can (in later Mathcad versions, anyway). See "Help", "Tutorials", "Features in Depth", "Temperature and User Defined Units" for more information.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you very much for the response. This is the best workaround I've seen to MathCAD's inherint inability display polar coordinates. Here is a screen shot of the applied function. I've added vectorally three complex quantities in polar (using Euler's formula). Predictably, MathCAD returns the answer in Cartesian. When I apply the function you sent me, it returns the answer in a two-element matrix, the upper quantity is the magnitude and the lower quantity is the angle, in radians. I think this will be a useful function for us. If only I could figure out how to return the angle in degrees instead of radians - any thoughts? Until then, we can convert to degrees with an extra step. Thanks again, and hopefully, someday MathCAD will add the coordinate system to either the worksheet options or the equation options.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ian Riensche wrote:
Thank you very much for the response. This is the best workaround I've seen to MathCAD's inherint inability display polar coordinates. Here is a screen shot of the applied function.
I find thay a very strange statement.
The functions I posted does exactly what you ask for.
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think the issue is only that your functoins are not defined in such a way they can be used in the units placeholder of a result.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think the issue is only that your functoins are not defined in such a way they can be used in the units placeholder of a result.
What was the secret behind doing that. I haven't seen that done before or requested on this forum.
Any other examples?
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The key is that you must have a function pair with the names, for example, "func" and "/func". If you put "func in the units placeholder of a result it applies "/func" to the results. There are some other examples in "Help", "Tutorials", "Features in Depth", "Temperature and User Defined Units".
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
There are some other examples in "Help", "Tutorials", "Features in Depth", "Temperature and User Defined Units".
Cheers
Mike
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If only I could figure out how to return the angle in degrees instead of radians - any thoughts?
This is the best I can do.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard, your MathCAD programming ability continues to impress me. Before you responded, I had modified your original function group to include a re-definition of the xy2pol() function, which I called, xy2p(). xy2p() does nothing more than convert radians to degrees in the same step that the angle is calculated. Please see the screenshot below. However, your approach does in two functions what mine took three to do. So again I thank you for your input.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It also leaves the polar function intact, so you can display in radians or degrees, depending on what is wanted.
Here's a very minor update. I don't know why I multiplied by 180/pi when I could have just divided by deg

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I've captured the points in the above posts for consideration for a future release.
Mona
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard Jackson wrote:
If only I could figure out how to return the angle in degrees instead of radians - any thoughts?This is the best I can do.
The choice of the base unit for Angle, has been another contested item in the Metrologia letters pages over the years, not just the 'is Angle a dimension?' question!
Doing the conversion isn't an issue as long as the unit is explicitly stated (within the units place holder, by the user or mathcad). If Angle were a dimension then Mathcad would positively indicate that its angular results are, by default, in radians, avoiding all these problems.
It is already possible to enter the magnitude & phase values using infix notation, but unfortunately it isn't that easy with the mouse clicks.
It doesn't help that infix isn't listed in the help menu (see postfix instead), however the angle sign is listed as a special symbol, and infix examples are given in the Custom operators quicksheet. All we need is an easy way of getting our chosen function inserted as an infix operator - perhaps a user pallette where we can place our quick access functions!.
There is a fundamental problem (for Mathcad) with values which have mixed units, because at the moment mathcad keeps only a single single dimensional factor for both halves of a complex number. This isn't a problem for cartesian representations (e.g. complex voltages = real + imaginary volts), but is a problem with a (magnitude + phase) representations where the magnitude part has volts as its dimensions, while the phase part has Angle as its dimension. Even if you are an adherent of 'Angles are dimesionless', you still have mixed units with magnitude+phase method within the same variable.
It could be an advantage for mathcad to be able to declare a structured variable such that the expected units of the different numeric components could be different, and checked. A complex number is such an implicit structured variable, but with the dimesions applied to the whole structure. In this case the electrical example of magnitude and phase internal representation for say line current, line voltage, and line impedance, with the usual computable relationship V=I.X (where X is the complex impedance). The complex algebra is well defined and understood, which is why we use it, but the other types can be a pain. (e.g. quaternions as a 4-vector, or as bi-complex, or a 2-vector of a scalar plus 3-vector, all of which are equivalent but with different implied calculation rules!).
Most of this is a confusion between (implicit) external representation and internal storage, just like 0.999999999999999999...
philip
Message was edited by: Philip Oakley This replies to the original comment about getting the number in the right units


